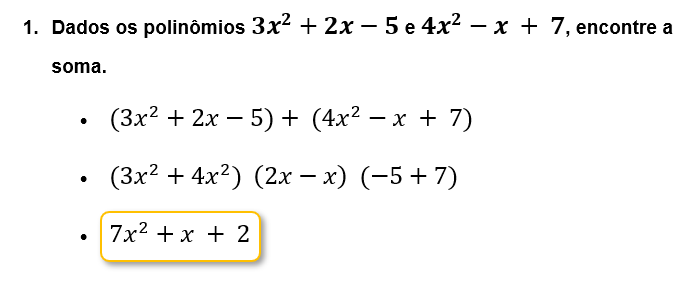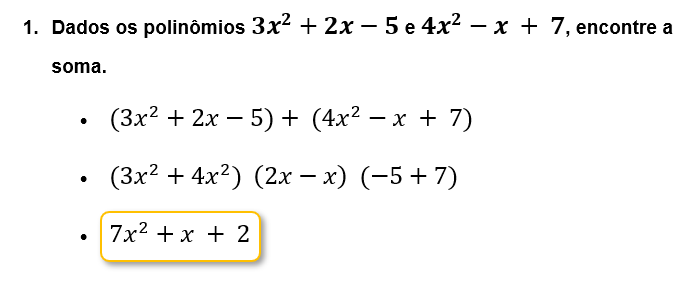Os polinômios são expressões matemáticas cruciais que emergem em várias disciplinas da matemática. Vamos simplificar o conceito de polinômios e compreender como trabalhar com eles de maneira acessível:
O que é um Polinômio?:
Um polinômio é uma expressão algébrica que envolve variáveis, coeficientes e expoentes. Geralmente, é uma soma de termos, onde cada termo é o produto de uma variável elevada a uma potência e um coeficiente. Exemplos de polinômios incluem 3x²+5x+2 e 2y²−7y−1.
Termos, Coeficientes e Grau:
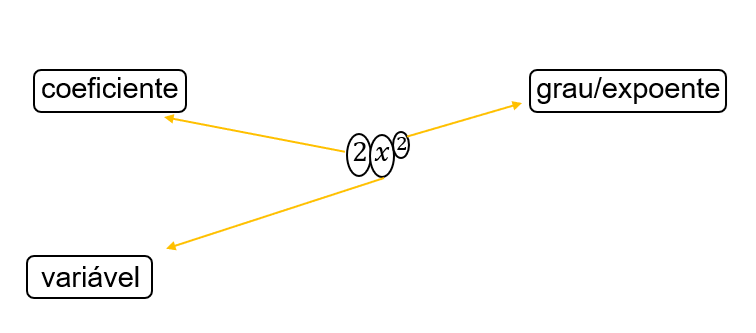
Cada componente de um polinômio desempenha um papel específico. Termos são as partes individuais da expressão; coeficientes são os números multiplicados pelas variáveis, e o grau é o maior expoente de uma variável na expressão. Por exemplo, no polinômio 3x²+5x+2, o termo 3x² possui coeficiente 3 e grau 2, o termo 5x possui coeficiente 5 e grau 1, e o termo 2 possui coeficiente 2 e grau 0.

Operações com Polinômios:
Realizar operações matemáticas com polinômios é essencial para muitas áreas da matemática. As operações básicas incluem adição, subtração, multiplicação e divisão de polinômios.
Adição e Subtração de Polinômios:
Para adicionar ou subtrair polinômios, agrupe termos semelhantes (termos com as mesmas variáveis e expoentes) e combine seus coeficientes. Por exemplo, para somar:


Multiplicação de Polinômios:
Ao multiplicar polinômios, use a propriedade distributiva. Multiplique cada termo do primeiro polinômio por cada termo do segundo polinômio e combine os termos semelhantes. Por exemplo, para multiplicar (2x + 3) por (x – 1), multiplique 2x por x e por -1, depois o 3 por x e por -1, e some os resultados.


Exemplo Prático:


Dicas Adicionais:
Ao fatorar polinômios, procure os fatores comuns a todos os termos.
A ordem dos termos em um polinômio não altera o seu valor.
Pratique com Diversos Exemplos:
A prática é fundamental para compreender e trabalhar eficientemente com polinômios. Resolva vários problemas para ganhar confiança e habilidade.
Conclusão:
Os polinômios são ferramentas poderosas na matemática, utilizados em diversas situações. Ao entender seus componentes e operações, você estará mais preparado para lidar com expressões algébricas complexas.
Exemplos Práticos de Polinômios: