A regra de três é uma ferramenta matemática poderosa para resolver problemas de proporção. Vamos descomplicar esse conceito para que você possa aplicá-lo com facilidade. Aqui está um guia passo a passo:
Identificando as Grandezas:
- Em um problema de regra de três, você terá grandezas já conhecidas e uma desconhecida. Identifique claramente as grandezas e suas unidades. Exemplos de grandezas: temperatura, dinheiro, velocidade, tempo etc. As grandezas podem ser Diretamente Proporcionais ou Inversamente Proporcionais.
Diretamente Proporcionais:
- Quando grandezas são diretamente proporcionais, quer dizer que quando uma aumenta, a outra aumenta também. Exemplo: Quanto mais bebidas o restaurante vende, mais dinheiro ele fatura. Se as grandezas forem Diretamente Proporcionais, multiplica-se em X.
Inversamente Proporcionais:
- Quando grandezas são inversamente proporcionais, quer dizer que quando uma aumenta, a outra diminui. Exemplo: Quanto mais velocidade, menos tempo demora para chegar ao destino. Se as grandezas forem inversamente proporcionais, multiplica-se em linha.
Dicas para interpretar:
- Se duas variáveis aumentam ou diminuem juntas, a relação é diretamente proporcional. Por exemplo, se o número de trabalhadores aumenta, e a produção também aumenta, é diretamente proporcional.
- Se uma variável aumenta enquanto a outra diminui, ou vice-versa, a relação é inversamente proporcional. Por exemplo, se o tempo para realizar uma tarefa diminui à medida que mais pessoas são adicionadas, é inversamente proporcional.
Exemplo Prático (Diretamente Proporcional):
- Vamos dizer que você está comprando livros e sabe que 4 livros custam R$ 80. Quanto custariam 7 livros? Aqui, podemos usar a regra de três:


Exemplo Prático (Inversamente Proporcional):
- Se um carro a 20km/h demora 5 minutos para fazer um trajeto, quanto ele demora se for a 30 km/h?


Dicas Adicionais:
- Lembre-se de manter as unidades consistentes.
- Confira se as grandezas são Diretamente ou Inversamente Proporcionais.
Pratique com Diversos Exemplos:
- A melhor maneira de dominar a regra de três é praticar com diversos exemplos. Encontre problemas do dia a dia e tente resolver usando esse método.
Conclusão:
- A regra de três pode parecer desafiadora no início, mas com prática, se tornará uma ferramenta valiosa. Esteja confiante ao enfrentar problemas de proporção, e lembre-se de que a prática leva à perfeição.
Exemplos Práticos de Regra de Três Simples:
1. Se 4 metros de tecido custam R$ 20, quanto custarão 8 metros?
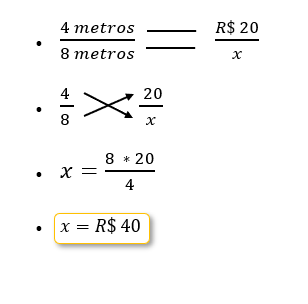
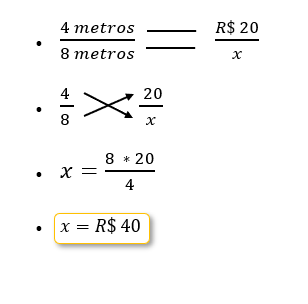
2. Se 3 trabalhadores constroem um muro em 6 dias, em quantos dias 5 trabalhadores construiriam o mesmo muro?


3. Se uma receita pede 2 ovos para fazer 12 cupcakes, quantos ovos são necessários para fazer 24 cupcakes?
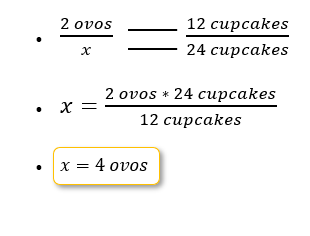
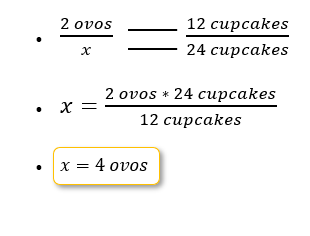
4. Se R$ 500 rendem R$ 50 de juros em um ano, quanto renderiam $750?


5. Se um carro faz 15 km com 1 litro de gasolina, quantos quilômetros ele fará com 20 litros?






