Analisar uma equação de primeiro grau no gráfico pode oferecer insights visuais poderosos sobre o comportamento das variáveis envolvidas. Vamos explorar como fazer isso de maneira fácil e detalhada:
- Entendendo a Forma Geral da Equação:
- A forma geral de uma equação de primeiro grau é y = ax + b, onde y é a variável dependente, x é a variável independente, a é a inclinação (coeficiente angular) da reta, e b é o intercepto y (o ponto onde a reta corta o eixo y).
- Identificando a Inclinação e o Intercepto:
- A inclinação a indica a taxa de variação da variável dependente em relação à variável independente. Se a é positivo, a reta inclina para cima; se negativo, inclina para baixo. O intercepto b é o valor de y quando x é zero.
- Desenhando o Intercepto e Aplicando a Inclinação:
- Para começar a desenhar a reta, marque o intercepto b no eixo y. Em seguida, use a inclinação a para encontrar um segundo ponto. Se a é 2, suba 2 unidades e vá 1 unidade para a direita a partir do ponto do intercepto, por exemplo.
- Desenhando a Reta e Identificando Tendências:
- Conecte os pontos marcados para formar a reta. A direção da inclinação indica o comportamento da equação. Se a inclinação for positiva, a reta sobe da esquerda para a direita; se negativa, desce. A magnitude da inclinação indica a inclinação da reta.
- Interpretando o Gráfico:
- O gráfico revela informações sobre a relação entre as variáveis. Se a reta é inclinada para cima, à medida que x aumenta, y também aumenta. Se inclinada para baixo, y diminui à medida que x aumenta.
Exemplo Prático:
- Considere a equação y = 2x + 3
- O intercepto é b = 3, então marque o ponto (0, 3) no eixo y.
- A inclinação a = 2, então, a partir desse ponto, suba 2 unidades e vá 1 unidade para a direita para marcar outro ponto (1, 5).
- Conecte os pontos para formar a reta.
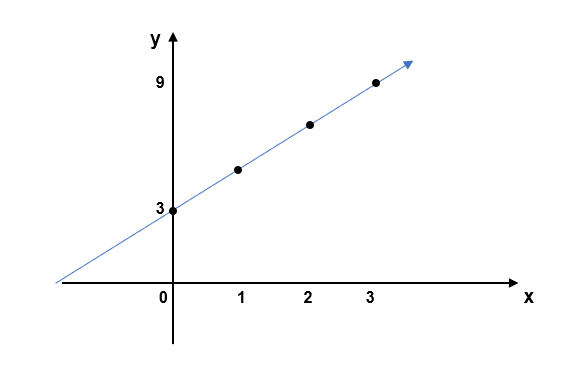
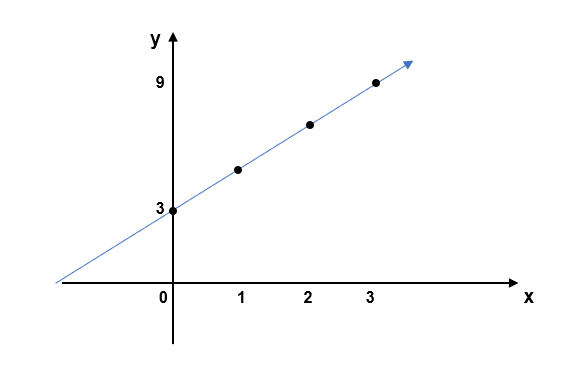
Dicas Adicionais:
- Se a inclinação for zero, a reta será horizontal. Se a inclinação for infinita, a reta será vertical.
- O gráfico fornece uma representação visual das relações entre as variáveis, facilitando a interpretação.
- Leia várias vezes o conteúdo e os Exemplos Práticos para fixar bem o conteúdo.
Pratique com Diversos Exemplos:
- A prática de desenhar gráficos de equações de primeiro grau é essencial para desenvolver habilidades de análise visual.
Conclusão:
- Analisar uma equação de primeiro grau no gráfico oferece uma perspectiva visual valiosa sobre a relação entre variáveis. Ao compreender a inclinação e o intercepto, você pode interpretar o gráfico com facilidade.
Exemplos de Análise de Equação de Primeiro Grau no Gráfico: